これまで、仏教の基礎である「唯識と空と縁」の話を記載してきました。
「なんだ、ただの宗教の話だったな・・」と割り切るようではいけません。
世界の普遍的価値(ワールド・バリュー)において、学問とは16歳以降に「神を信じるか、信じないか」で、
前者は神学(数学・哲学)へ、後者は近代学問(※)に分かれるのです。
※
近代学問(=近代科学)には、自然科学と社会科学の二種類がある。
自然科学:人間が作ったものでないもの(神が創造したのを研究する学問)
社会科学:人間が作ったもの(人間が集団で作ったものを研究する学問)
この二種類は日本の文系・理系の分け方に似ているが、対立するものではない。
それ以前は、初頭学問の文学・人文学・歴史学・言語学・音楽・論理学・修辞学などのリベラル・アーツ(一般教養)という学問基礎を学ぶのです。
だから全ての学問体系は、神学と科学に分かれる前は、根っこで繋がっているのです。
日本では、中高教育で、
文科系(目に見えないもの=非科学=悪) vs 理数系(目に見えるもの=科学=善)
なんて間違った分け方をして、
更に大学教育においても文学部○○学科なんてやるのは、もはや”学問犯罪”と言って良いです。
逆に『我こそは理数系。我こそ神(科学)の代弁者なるぞ。みんな私の言うことを聞け。』と言って、何かの教祖にでもなったが如く聖書(理科系の教科書)を片手に、唯物論を振りかざし、拝金主義や虚無主義や自虐的な破滅・嗜虐主義で、神経症的な学歴成績競争を推進していく輩(やから)がいるからどうしようもないのです。
理科と数学は全く対立するものなのです。理科は近代学問、数学は神学に属します。
学力や偏差値云々以前に、世界の国際基準から笑われるほど土台が間違っているのです。こんな状態だから、勉強が楽しいと思えなくて当たり前です。
ここからは仏教理論が、いかに近代科学の先駆けであり、スゴイかという話をここから書いていきます。
驚くべきは、この2000年前の仏教理論に、現代の科学が、やっと最近になって追いついてきたということです。
形式論理学、記号論理学、ユークリッド幾何学も同様ですが、まず行う作業とは定義を決めることです。
直線とは何か、三角形とは何か、という定義を述べてから、公理という命題を作ります。
その公理から様々な定理を導き出します。
これが完全理論と言われる、初めに定義を書く学問体系です。
この体系に疑問を抱いたのがマックス・ウェーバーです。
マックス・ウェーバーは資本主義の祖として言われています。(実際は大嘘でキリスト教のプロテスタント運動というルターの抑圧解放の精神が作った。ちなみに日本では仏教の精神を最初に伝えた聖徳太子が資本主義の祖です。)
彼は初めに資本主義の定義を下すことはせず、議論を終えてから定義を下すという態度を取りました。
なぜなら、資本主義らしきもの、つまり資本主義モドキのようなものが多数存在するために、定義を満たすだけの条件整理が出来ておらず、その状況下で定義付けをすると真相の解明に支障を来すからです。
まずはそういった条件を全部整理した上で、本質を解明して定義を下そうとするのがウェーバーの考えでした。
実はこの考えは現代数学にそっくりです。
最新の数学の手法は、まず無定義要素、つまり何も定義しないところから始まります。
点・線などの定義付けを何も行わず、無定義のままの要素を用いて公理を作り、定理を導き出すのです。
向いて意義要素の本質は、無定義のまま、仮にそういうものとして考えておく、いわば”仮想のもの”です。
有名な例を一つ挙げておきます。
300年頃にギリシャの数学者のユークリッドの始めたユークリッド幾何学(きかがく:点と線などから公理を導き、その後にいくつもの定理を導く)の5つの公理というものがあります。
1「二点を結ぶ直線はただ一本のみ」
2「任意の線分は延長できる」=1と2を合わせて「二点を通る直線はただ一つ」という意味。
3「円は任意の点と任意の半径で作図できる」=コンパスを使うことへの許可
4「すべての直角は等しい」
問題なのが5つ目で、
5「一直線が他の二直線と交わってできる角のうち、同じ側にある二つの内角の和が二直線より小さければ、この二直線は限りなく延長するとついには交わる」
=現代的に言うと、
「二直線が一直線と交わっているとき、もしその同じ側にできる内角の和が二直角よりも小であったならば、二直線はその側へ延長すれば必ず交わる」
「直線外の任意の一点を通って、これと平行な直線がただ一本だけ引ける」(下図↓)
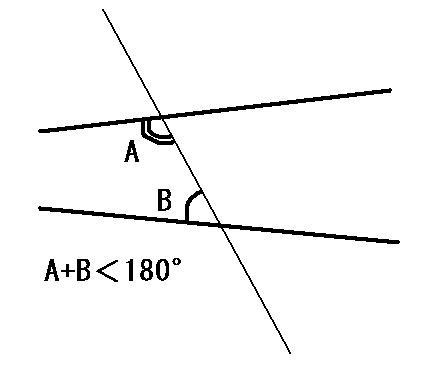
例えるならば、無限に続く2本の線路の片方に立って、はるかかなたを眺めてみる。
すると、自分の立っている線路は真っ直ぐ見えるが、片方の線路は曲がって自分の線路の方に近づいてくるように見える。あるいは地平線が曲がって見える。

この線路の平行線は本当に交わっていないのだろうか?
ぶっちゃけ、どこかで交わっているのではないか?
地平線はどう見ても曲がっているが、あの地平線の先まで2本の平行線を引いたら、地平線だけが唯一1本だけの平行線と言えるのだろうか?
ここで数学者は、この第5公理は、この第5公理を残りの第4公理を使って証明しようと躍起(やっき)になりました。
しかし、誰も成功することはありませんでした。
そして19世紀になって、ロシアの天才数学者ロバチェフスキー(1792~1856年)が、帰謬法(ある命題Aを証明するのにAでないという前提からは矛盾が生ずることを示して行う証明法。背理法とも言う。)を用いて、第5公理を否定して幾何学を構築すれば、どこかで矛盾に突き当たるだろうと考えました。
具体的には「一直線外の一点を通ってその直線に平行な直線は一本とは限らない」と仮説を立てたのです。
今までのユークリッド幾何学の公理は、
・直線 L 上にない1点 P を通って L に平行な直線は1本しかない
・三角形の内角の和は180°
でした。
そこでロバチェフスキーは、「平行線は交わらない」という、ユークリッドによる”定義”を否定し、「平行線は無限の彼方で交わっている」とすることによって、
・直線L上にない1点Pを通ってLに平行な直線は無限に存在する(1本だけとは限らない)
・三角形の内角の和は一定しない。
と仮定しました。
しかし、いくら考え勧めてもこの仮説が全く矛盾に突き当たることなく、一つの体系が出来てしまいました。
これが「非ユークリッド幾何学」です。
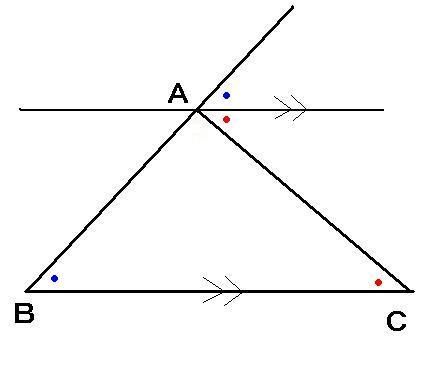
今も中学校の数学で習う「三角形の合同条件」にある「三角形の内角の和は180°である」というものがあります。(下図↓)
三角形ABCに、点Aを通る辺BCに平行な線を引きます。
すると平行線に対して青い角の同位角は等しいので青い角度は同じです。
また錯覚は等しいので赤い角度も同じです。
よって、三角形ABCの内角の和は180°です。
し か し こ れ も 実 は 嘘 だ っ た の で す 。
内角の和が180°じゃない三角形は、実際に作ることができてしまいます。
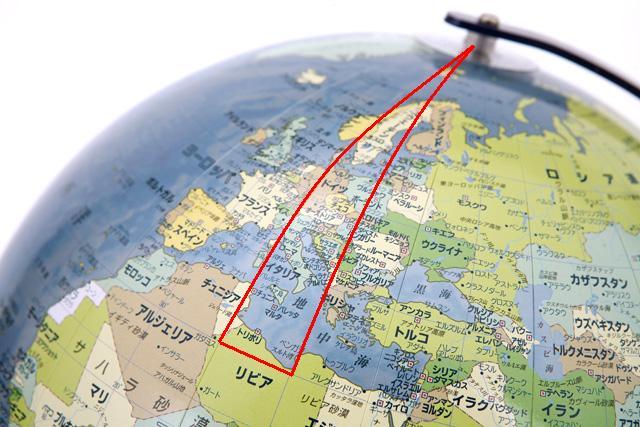
例えば、地球儀で北極点に立って、経度に沿って真っ直ぐ進み、途中で直角に折れて、また真っ直ぐ進み、また途中で直角に折れて北極点に戻ると、三角形が出来ます。(下図↓)
しかし、直角(90°)に2回も曲がった時点で、内角の和が180°を超えてしまうのです。
北極点の角度もゼロではなく、仮にX°(X>0)としても(X+180)°で180°より大きくなります。
ネタバレすると、これは”曲面上で平行線を画いたから”です。
真っ直ぐ進んでいた自分は、真っ直ぐに平行に進んでいたと思い込んでいただけだったのです。
だから”どんな三角形でも”内角の和が180°になる(=直線外の任意の一点を通って、これと平行な直線がただ一本だけ引ける)というユークリッドの公理は大嘘と言うことで、大崩壊したのです。
「三角形の内角の和が180°である」というのは、実は”平面上でのみ”成り立つということが分かりました。
これは科学史上の一大事でした。
それまで自明の真理であると思われていた公理が、実は真理ではなく、一つの『仮定』にすぎないということが明らかになったのです。
ユークリッドの5公理を元に計算して、地球儀を描くと、地図がとても変な形になって、航海に出た時に迷ってしまう理由も解明されました。
ニュートン力学も、慣性の法則も、運動の法則も、作用反作用の法則も、絶対の真理として捉えていたものが実は”仮定にすぎない”と明らかになりました。
数学や物理学だけでなく経済学も同じことです。
かつては経済の法則は絶対真理として信じられており、だからこそマルクス主義のマルキストなどはマルクス理論を理解しない輩(やから)は皆殺しにすべき、などと極論していました。
(マルクスの「宗教はアヘンである」という言葉を崇拝して「科学崇拝・科学万能主義者」が生まれました。中国では中国共産党の毛沢東が1960年代以降「文化大革命」で、目に見える物質以外を信じる非科学的な連中を重軽傷者合わせて1億人以上の歴史上最多の大虐殺をしました。今でも中国国内だけでなくチベットやウイグルで盛大にやってます。日本でも1960年代、集団リンチで大量に身体障害者を量産した学生運動・大学闘争、その残党の過激派の赤軍派・革マル派と呼ばれる集団が起こした浅間山荘事件・よど号ハイジャック事件、この極左の流れが後にサリン事件で有名なオウム真理教になりました。この世代は大変に勤勉だったので、現在では大学教授や教師などの教育関係者、医者、弁護士などになっている人が多くいます。そして彼らは、科学崇拝・宗教撲滅・国民は法律でガチガチ規制すべき・福祉国家は最高・科学を語る自分の言うことだけ信奉しろ、を理想とする人が多くいます。ついでにだからこそ共産党がバリバリの理科系で、弱者救済で無駄に正義感と革命意識の強い人が多いのです。)
しかしケインズ理論が理解されて、どの理論も一つの”モデル(仮定)”に過ぎない、ということが一般的になって、ケインズ理論の登場で一度排斥された古典派も復活しました。
そして90年代になって、理論経済学に至り、
ケインズ(国が法律で市場を規制していくべきだとする左翼系の経済理論)や、
古典派(市場を法律で規制するのはよくないから、規制緩和して自由競争にすべきだとする保守右翼系の経済理論)
だけでなく、経済理論は特定の仮定の下に成り立っているモデルなので、対比して研究すべきという認識が常識になりました。
日本人のための宗教原論―あなたを宗教はどう助けてくれるのか
数学嫌いな人のための数学―数学原論